George Rebane
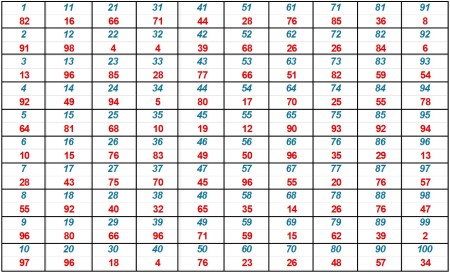
OK boys and girls, it’s time to take a break from our socio-political harangues and debates, and delve into something more intellectual yet delightfully accessible. The figure contains a 10-by-10 network of nodes each identified by their blue numbers from 1 to 100. The related red numbers denote the cost of traversing that node.
The problem to be solved is to identify the minimum cost path between a given starting node and a destination node. Here, let’s arbitrarily say we wanted to start on node 19 and end on node 92. What is the path or sequence of nodes to be traversed that minimizes the total cost of the trip when all the costs of the visited nodes are added up? And as you puzzle on the solution, see if you can come up with an algorithm that can solve all such problems.
The rule for traversing is that allowable steps for any given node are the eight or fewer of its neighboring nodes. For example, from node 25 you can step to nodes 14, 24, 34, 15, 35, 16, 26, 36; and from node 31 you can step to 21, 41, 22, 32, 42.
This is a simplified yet still powerful version of a problem that I had to solve long ago on a contract to develop an interactive combat system for combined arms field operations. The specific problem was to compute and display a minimum time feasible path across a region of complex terrains for a given make-up and size of a combat unit to get from their current location(s) to a selected location. Today a version of the resulting algorithm is used in you car’s and cell phone’s route calculating apps. Have fun and let us know your solution and algo.


Leave a comment