George Rebane
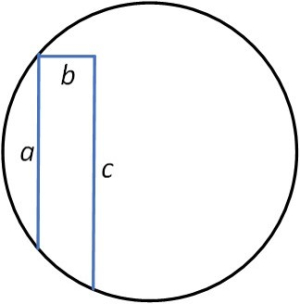
As a fun diversion, here’s your Easter Egg problem albeit with a round egg. Given three mutually perpendicular line segments of lengths a, b, c, as shown in the figure, Problem: (A) derive the expression for the radius r of the circle, then (B) for (a, b, c) = (13,6,18) calculate the value of r.
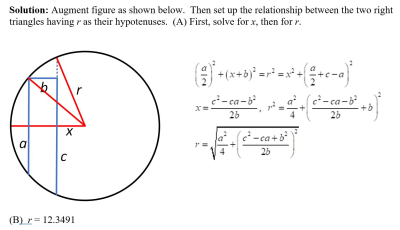
[23apr25 update] My solution is shown below.


Leave a comment