George Rebane
For a little relief from the travails of the election season, I offer a little bagatelle for your intellectual entertainment – something provided by neither candidates nor commentators during these last couple of years. This jumped from my fevered brain one night as I was noodling over some candidate problems for Techtest 2025 coming up next spring.
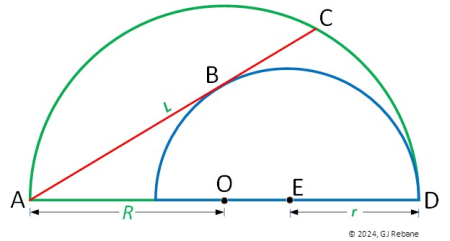
From the figure we see a green semicircle of radius R with center at O in which resides the smaller blue semicircle of radius r with center at E anchored, as shown, on the right end D of the large semicircle’s diameter. From the left end A of the diameter issues the red line AC which is tangent to the small semicircle at B and terminates on the circumference of the large semicircle at C. The only data available is the value of R. The task at hand is to find the value of r and the length L of the line which is equal to the perimeter length of the small semicircle, or demonstrate that no such solution is feasible.
At an appropriate time in the future I will append this post with the solution, and also give you immediate feedback if you post your solution as a comment or email it to me.
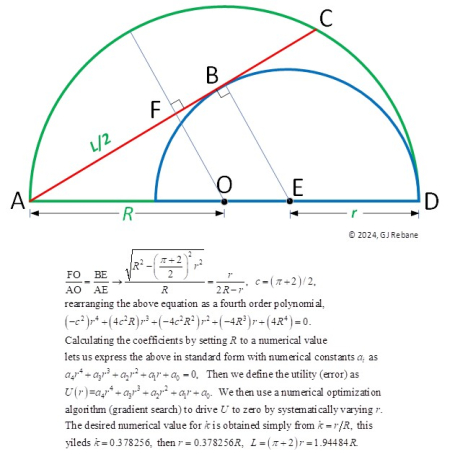
[4nov24 addendum] Well that didn’t take long; we have some very astute readers led by Efox who submitted the correct solution in his 232pm comment. What made me smile was the description of his approach using Excel™. We would call it the direct bigger hammer method. He correctly argued that a solution is indeed feasible and immediately recognized the scalability of the problem which allowed him to deduce that r must be a fixed fraction k of the given radius R – i.e. r = kR. He then extracted a relevant algebraic equation from the geometry that contained both R and r – see the first equation below the figure. Realizing that an analytical solution for r would be too tedious to pursue, he got out Excel and used his bigger (“old fashioned”) hammer by inserting a numerical value for R and then kR for r, and then started incrementally varying k until his equation was satisfied with the k interpolated to yield at least a five-place decimal accuracy. Bravo.
Being ever the dilletante, my approach took longer. I began with the fervent belief (unfounded hope?) that there would exist a compact and elegant formula that yielded k, recognizing that triangles AFO and ABE are similar, and a little algebraic manipulation would produce the desired result. No such luck. The best that could be done was to recognize that the obviously equal algebraic ratios shown below could at best be mangled into the standard form of a quartic polynomial in r as shown in the figure below. And to solve that for a positive real root from which k could be extracted would indeed be equivalent to getting into a land war in Asia (I refer you to the 33rd edition of the iconic CRC Standard Mathematical Tables and Formulas (2018), p74).
The numerical optimization algorithm I used is one of the tools in the Solver add-in of the Excel spreadsheet. Solver is a very valuable part of that spreadsheet, and when installed is accessible under the ‘Data’ tab. The tool can be used for everything from solving equations (like above) to finding ‘best’ values for certain input parameters such as corporate ‘operating points’ with complex cashflow models. It has been a lifesaver for me over the years, and I could wax eloquent over its manifest benefits. But alas, such accolades are out of scope here.


Leave a comment