George Rebane
All socio-economic problems depend on their numbers, not understanding these replaces reasonable discussion with emoting.
The ‘great replacement conspiracy’ is the latest kerfuffle to rise to national prominence. The Left is accusing the Right of fostering this theory of dark-skinned immigrants and illegal aliens being welcomed into America to outvote and outbreed the European-descended whites. (more here, here, here, here) History tells us that such replacement concerns first started in France long ago, and in the US ascendant Democrats have crowed for years, and continue to do so today, that the Republicans are being replaced as their party shrinks. But no matter where it started, the point I want to develop is that in our innumerate nation, almost everyone today is ignorant of what replacement means and really is. And the evil party is using this ignorance to continue to divide us. So let’s clear up some cobwebs in order to correctly assess what all the fuss is about.
The general notion of replacement requires first and foremost the existence of a defined ‘container’, be it a region of square miles full of people, a jug that can hold fluids, or a bowl containing different colored marbles. Given the container, we now have to consider two distinct cases. Case1 in which the container has a not-to-exceed carrying capacity, and Case2 in which the container’s carrying capacity is not limited.
Case1. Suppose we have a small bowl that can hold five marbles, and to start, it contains three Amarbles and two Bmarbles. We all understand that if Bmarbles are reduced to one by adding one Amarble or one Cmarble, that Bmarbles are being replaced both in their absolute number and in their share of the bowl’s contents (going from 40% to 20%), now leaving the A, B, C marble count at 3, 1, 1 respectively. No one should have a problem understanding this kind of replacement.
But is it possible for replacement to occur if a categorical population (e.g. Bmarbles) remains unchanged or even increases? Well yes, this gives us Case2 where we suppose Amarbles increase by two to five, Cmarbles double to two, and Bmarbles remain unchanged at one. Now the share of Bmarbles has dropped from 20% to 1/8 or 12.5%. The Bmarble share has definitely been replaced by the greater shares of Amarbles and Cmarbles.
The more interesting Case2 scenario is when the number of all three kinds of marbles increases over time. Let’s suppose that Amarbles increase at the rate of 4/year, Bmarbles at 1/year, and Cmarbles at 3/year. If at the beginning of the year we had A, B, C marbles numbering 3, 1, 1 respectively, then at the end of the year they would number 7, 2, 4. So focusing on Bmarbles, we see their number double, but their share drop from 20% to about 15%. Again, Bmarbles had 5% of their share replaced by the population increase which was taken up by the shares of Amarbles and Cmarbles. So it’s easy to see that replacement can take place in populations that also increase over time, but only at a rates lower than that of the other population cohorts.
Let’s now go from marbles to people occupying a landmass that has no clearly set capacity. Say, there are 100 million total people now divided into cohorts of Apeople, Bpeople, and Cpeople in shares 20%, 50%, and 30% respectively. (Time to fasten seatbelts for the arithmetically challenged.) Population will be affected by birth rates, net immigration, and death rates. From numerous demographic studies over the years we know that the population of a cohort will be stable or remain unchanged when its fecund women give birth to 2.1 offspring in their lifetime – the so-called replacement rate. For our purposes, we’ll assume that women are fecund in their 20 to 40 year age range, or about 17% of the population (based on 2020 US demographics).
The mean annual birth rate per woman over her 20-year fecundity is her mean number of offspring divided by 20. For a stable population that rate is 2.1/20 = 0.105 births per year per woman. Now the astute reader will also recognize this as the nominal annual death rate across all ages. To illustrate with some numbers for our 100 million population, we will have 17 million fecund women producing 17,000,000*0.105 = 1,785,000 babies per year. And this is the same number of people who die each year giving the population birth rate and death rate equaling 1,785,000/100,000,000 = 0.0179 per person in the population. With this little piece of arithmetic under our belts, let’s now take a more detailed look at our population scenario.
Suppose, in our population the birthrates for fecund women in the A, B, and C people are 2.5, 1.5, 3.0 offspring per fecund woman. Doing the same calculations now for population cohorts of Apeople = 20 million, Bpeople = 50 million, Cpeople = 30 million each having 17% fecundity in their populations of 3.4e6, 8.5e6, 5.1e6 respectively. (To save space and provide clarity, from here on I’ll use the compact exponential notation for numbers where 3,400,000 = 3.4*10^6 = 3.4e6, and 0.0179 = 1.79*10^-2 = 1.79e-2. This is what scientists and engineers use to express both big and small numbers and enable rapid mental math to do simple calculations.)
So now, the birth rates for each cohort are Arate = 2.5/20 = 0.125/year, and similarly Brate = 0.075/year, Crate = 0.150/year. Going through the same math, we get the annual number of births of Ababies = 3.4e6*0.125 = 425,000, and similarly Bbabies = 638,000, Cbabies = 765,000. Deaths for each cohort are Adeaths = 20e6*0.0179 = 357,000, and similarly Bdeaths = 893,000, Cdeaths = 536,000. This yields a net population change for each cohort of Achange = 425e3 – 358e3 = 67,000, and similarly Bchange = -257,000, Cchange = 228,000.
Adding these net changes to the initial population numbers, we get the new cohort populations after one year as Apop = 20e6 + 67,000 = 20,067,000, and similarly Bpop = 49,743,000, Cpop = 30,228,000, giving the new one-year total population of 100,038,000. The new population shares are then Ashare = 20,067,000/100,038,000 = 20.06%, and similarly Bshare = 49.72%, Cshare = 30.22%. So it is clear that 0.28% of the B cohort’s population share was replaced by the increased shares of the A and C cohorts. This, of course was due to the drastically low fecundity rate of the B cohort at 1.5, or 0.6 below replacement rate, while the other two cohorts’ rates were above the 2.1 replacement rates. BTW, these rates are pretty close to some actual fecundity rates, especially the B rate approximating the Anglo rates for the EU and US.
To see the longer term impact of the above scenario, we must now replicate all that math for the next year, starting with the new population shares. And this iteration can be carried out for longer time horizons of say 25 or more years to see the significance of how different population cohorts replace one another over time.
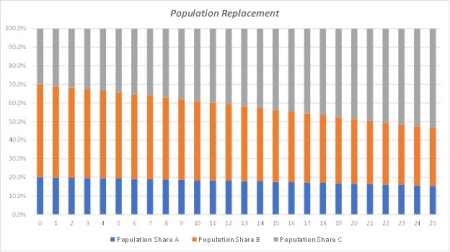
What we’ve ignored so far is net immigration that varies over the population cohorts. As an example, say the net immigration rate of 3% people in the first year is concentrated in cohort C. This gives that cohort an added 900,000 starting annual population increase that significantly impacts its population share, and hence its contribution to replacing other population cohorts. I developed a spreadsheet model of all this to generate the population share chart shown below which clearly illustrates the replacement phenomenon.
Over a 25-year period, using the above parameters, the population increased by 41.3%. Were this increase applied equally to all starting cohorts, then the A, B, C populations would grow to 28,270,000, 70,675,000, 42,405,000 respectively. However, after 25 years the A, B, C cohort populations shares were 15.4%, 31.1%, 53.5% respectively yielding populations of 21,771,202, 44,000,314, 75,577,673. This shows that cohort C’s excess population growth of 33,172,673 replaced 6,598,798 and 26,674,686 of cohorts A and B respectively.
Coming back to today’s politics, the Great Replacement, bragged about by Democrats and which outrages Republicans, is a real concern to the extent that our open border invites people by the millions to enter illegally, gain citizenship, and overwhelmingly vote for the party that facilitated their entry and subsequent amnesty. Denying that this is happening is yet one more Big Lie from the evil anti-American party.
[21may22 update] “Watch out for odious theory” The letter of a Lee Freidenfelt in the 21may22 Union again underlines how sadly deficient is the progressive mind. S/he, like all leftists, doesn’t understand the cultural replacement process in a society, and thinks that those who do and therefore lament the illegal and rapid dimensions of replacement are ‘peddling incredibly dangerous ideas’, and, of course, should be censored in our newspaper. Like so many of his unfortunate ilk, Freidenfelt thinks that believing in the so-called Great Replacement Theory is racist and fomented so that “every time minority groups seek representation in government to address their issues”, we have “a reactionary backlash from the hegemonic powers that drape themselves in the flag with a romanticized perspective of American/German/Italian values of the old ways.” Those who pay attention know that ‘replacement backlash’ has nothing to do with legitimate citizen minority groups voting for their preferred representatives. The country’s Freidenfelts draw a strong causal connection from such “incredibly dangerous” replacement reports (like mine) to “what happened recently in Buffalo, New York, and countless other racially motivated hate crimes in our country.”


Leave a comment