George Rebane

The recently launched Webb space telescope will be able to peer further back in time and see more of what was then there.  As an amateur cosmologist, I’ve been interested in this new instrument for some years now.  It brings these new capabilities to bear because of its very large mirror and that its imaging plane is designed to be sensitive to infra-red light.  From high school we recall that IR has a long wavelength, and therefore can penetrate through all kinds of dust, water vapor, and other tiny stuff in space.  It’ll be able to make out far-off galaxies through dust clouds that formed around 13.5B years ago, only 300M years after the Big Bang.  (more here)

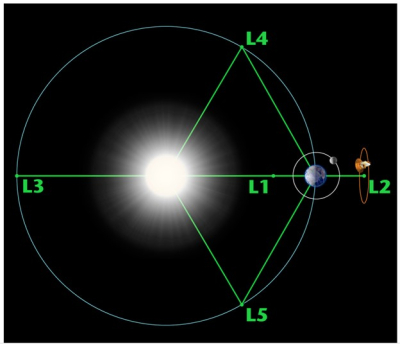
In the media we have been told that the Webb will orbit Earth’s L2 point shown in the above figure which also indicates the location of the other four Lagrange points.  The L2 point is on the straight line connecting Earth and the Sun, and reported to be about a million miles beyond Earth’s orbit.  Since this point in space stays on such a straight line, the angular rotation of L2 therefore equals that of Earth; along with our planet, it completes one rotation of the Sun in 365.25 days.

The Lagrange points are unique locations in a three-body configuration where the gravitational attraction of the two larger bodies provide ‘stable’ orbital points for much lighter third bodies.  Of the three kinds of stability – conditional (marble on large ball), unconditional (marble in a bowl), neutral (marble on a flat plane) – only L4 and L5 are unconditionally stable in that if a lighter body there is perturbed, it will remain in the L4 or L5 region (cf. The Travelers of Jupiter).  The other three points are conditionally stable, a perturbation from, say, the solar wind or the gravitational effects of the other planets, will push the lighter body away on a trajectory never to return.  Hence, to keep the Webb telescope near L2 requires little accurately directed squirts of thrust now and then.

Ever since I was a physics major, I was always intrigued by the balance of forces that gave rise to the Lagrange points, but having solved a number of other multi-force problems in my studies, I never took the time to actually calculate and confirm the existence of these counter-intuitive stable points in orbital mechanics.  But the launch of the Webb got me off my duff, and I decided to take a closer look and see what was required for the L2 to exist and how far was it really from Earth – a “million miles” sounded a bit too coincidental.

So, from the figure, let the Earth-to-L2 distance be r_EL2.  For any kind of stability, at the L2 point we must have its centrifugal force outward equal the sum of the Sun’s and Earth’s gravitational forces inward (toward the Sun and the Earth).  We can compute the actual value of r_EL2 from some straightforward formulas, namely Newton’s gravitational attraction and the centrifugal force formulas known from physics.  I show this derivation in the panel below.

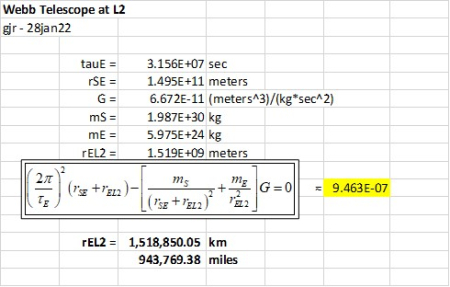
But first we need to define the terms.  The m_x are the masses for x = Sun, Earth, Webb at L2.  The r_x are the respective distances in the three-body orbital plane.  G is the gravitational constant in Newton’s law of gravity, and τ_E is Earth’s orbital period (one year) around the sun.

These calculations, along with the proper values for all the terms, are shown in the spreadsheet figure below.  The astute spreadsheet driver will note that I used Excel’s nonlinear gradient search feature in its ‘Solver’ function to solve for the value of r_EL2 that drives the equation in the box to zero – i.e. the left-hand side is the ‘utility’ to be minimized by the correct value of r_EL2; its minimized value is highlighted in yellow.  (This saved me from having to produce the analytical solution for a cubic equation – discretion is the better part of valor.)

And there you have it.  The Earth-L2 distance is actually 943,769 miles, and not the nice rounded one million miles – a 6% error.  And BTW, my calculated values agree with what’s published in the literature, so there.  Newton still rules for these kinds of calcs.