George Rebane

Governments here in America and around the world are fumbling around with Covid response policies as every new variant is discovered and infection cases surge and retreat.  People continue to be assured that the public agencies and their political leaders are “following the science”, even when there is no evidence of such following presented or demonstrated.  But as we have all experienced, the government agencies, ‘experts’, and politicians are all over the place with their advice, prescriptions, and mandates.  It is clear that neither the national nor global collective knows how to properly respond to the pandemic (e.g. here)  More disturbing are the ongoing subterfuges that leak out in the media and online.  An extremely revealing and disturbing interview is by Tucker Carlson of Robert Kennedy Jr, author of the current best seller The Real Anthony Fauci (2021).  It has been pulled by YouTube and FN, but is still available on Bitchute here.

In my many-years experience with healthcare decision making, I have found that practitioners in the medical industry are profoundly ignorant of uncertainty, risk, utility, estimation, and in general critical interventions that are affected by uncertainties (i.e. depend on probabilistics).  This assessment applies especially to the physicians with whom the patient interacts.  These people are uniformly condescending or arrogantly hubristic in how they hide their ignorance of the maladies in question, and what is required for the lay patient to make a reasoned and understandable decision.

Perfidy aside, nowhere is such practice more visible to the technically trained than in the field of public health.  A current posterchild demonstrating this is how little and erroneously we are informed about Covid testing.  We are told that testing is somehow critical to reducing the spread of the disease – the more testing the better.  Tests are communicated to the layman as consisting of one uniform process that somehow reliably determines your infection status AND your ability to infect others.  Science tells us nothing could be further from the truth.

Ignorance of causes and effects should be usefully represented quantitatively.  Such ignorance is no excuse for avoiding quantitative decision support techniques.  For example, here is an AMA article that talks about test types, dependers, and whyfors, but gives you no information about the involved probabilistics (e.g test sensitivities and specificities) for decision making.  Today machines can be designed to incorporate more knowledge than any one or group of practitioners can manage in literally any specific domain of expertise.  As a consequence, where such technology is applied, AI-based decision support systems outperform their human counterparts every time – and this is specifically the case in medicine and healthcare.  Here is Nobelist Daniel Kahneman on AI bettering human decisions. (here and here)

To illustrate the spread of our collective ignorance and hysteria, I want to return to a robust example from Covid testing.  In these pages I’ve devoted a lot of time and real estate to presenting the quantitative factors that relate to Covid test results, and their impact on the utility of such testing.  Testing is usually performed for two reasons – to measure the spread or penetration of a disease in a target population, and to determine whether a specific individual has been infected.  Recall that no test is perfect, and the reliability of a medical test is given by its sensitivity (probability that the test comes back positive when you do have the disease), and specificity (probability that the test comes back negative when you don’t have the disease).  Last year I posted ‘Testing, testing, testing – Really?’ which contained the following example.

(Recall that the minus sign with the hangy-down part, like this ¬, means ‘not’.  So ¬TP means ‘not Test Positive’ or simply a negative test result.  Similarly for ¬V, which means ‘not virus’ or not infected.)

We start with the prior probability that the asymptomatic walk-in has the virus which computes to about P(V) = 100K/330M = 0.0003 assuming generously that today about 100K Americans have been infected as opposed to today’s reported number of 42K.  The test’s likelihood ratio L(TP|V) = P(TP|V)/ P(TP|¬V) where V stands for virus present, ¬V means virus absent, and TP indicates Test Positive.  So the ratio is simply the two probabilities of a positive test given that the virus is present and the virus is absent – i.e. ¬V.  What we want to calculate is the updated or posterior probability that a person has the virus given that the test came back positive.  The Bayes formula for that is P(V|TP) = L(TP|V)P(V)/[L(TP|V)P(V) + 1 – P(V)].  Using the published numbers P(TP|V) = 0.60, and P(TP|¬V) = 0.25 (rough average of quoted range), we get L = 2.40.  Plugging this into the Bayes formula gives us

P(V|TP) = (2.4)*(0.0003)/[ (2.4)*(0.0003) + 1 – 0.0003] = 0.00072.

This tells us that an asymptomatic walk-in testing positive more than doubles his probability of having been infected, but his overall probability of actually being infected is still ridiculously low.  So what are you as a medical professional going to do with that information?  The answer is nothing much, because his probability of being uninfected, even with testing positive, is still P(¬V|TP) = 1 – P(V|TP) = 1 – 0.00072 = 0.9993, almost certainly virus free.

Now what happens when the test comes back negative; what’s the probability P(¬V|¬TP) that individual is actually not infected.  Sparing you the math, the answer is P(¬V|¬TP) = 0.9998, or almost certain that the individual is not infected.  So now you have two almost certain probabilities (0.9993 and 0.9998) that there is no infection present regardless of whether the test came back positive or negative.  That is the dirty little secret that no one wants to tell the public, because it reinforces the naked truth that the objective here is control and not ‘following the science’.

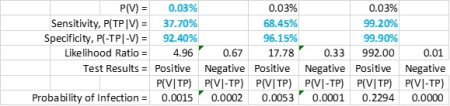
I dug up some current data on antigen tests for Covid.  The cited antigen test parameter ranges are – sensitivities P(TP|V): 37.7%-99.2%, specificities P(¬TP|¬V): 92.4%-100% (here).

If we also include the averages of these data and compute the chances that any given walk-in has Covid, regardless of their test’s outcome, then we can summarize these in the table below.  Clearly it demonstrates the futility of using single test outcomes to make healthcare decisions for the tested.

From the above table, note that even with the almost ‘perfect’ (rightmost) test, we can conclude that a positive test result yields little more than one-in-five chance that the walk-in has the virus.  The less perfect and more realistically performing tests yield extremely low probabilities of infection no matter the test result.

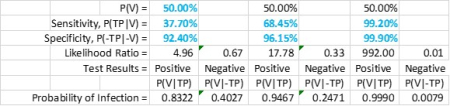
On the other hand, if we claim prior ignorance of infection for the tested, the results below show that again only the high-performance rightmost test gives reasonably reliable results.  The lesser performing positive test results may be of some use, but fail miserably when returning a negative result.  If we can make a case that each test gives an independent result, then multiple tests may be of some use if their results concur.  But the bottom line of all such testing is that, at best, it only provides a marginally useful snapshot of the patient’s infection status which can change the moment exposure is resumed.

Having examined such results, which are not discussed in the MSM, the question still begged is revealing the real purpose of administering such tests for determining the public’s access to events, transportation, and schools.

For completeness, I list below some major RR commentaries and analyses of testing as applied to the current Covid pandemic.

‘The Value of Testing’

‘Testing- One mo’ tahme’

‘The Reliability Roulette of Testing’

‘Covid Testing – Unclear on the Concept’

‘The Real Value of Unreliable Tests and Testing’

‘Testing to determine population fractions’

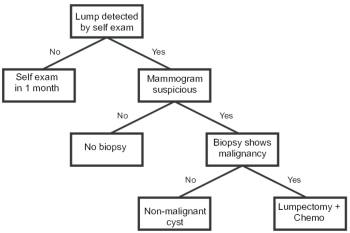
[Addendum]  Absence of Covid symptoms decision trees is a very clear indication that the medical industry has no clear or unified idea as to how lay people should respond when they believe they have Covid-like symptoms or have been exposed to Covid.  Decision trees have been used to teach diagnostic processes in all fields, not only in medicine.  And they are the standard vehicle for capturing and communicating such diagnostic and ‘repair’ processes.  Decision trees are very machine programmable, and have been used in automated (e.g. ‘expert’) and interactive diagnostic and maintenance systems for decades.

The above figure shows a simple breast cancer screening decision tree.  Much more complex trees with multiple branches (higher arity) from every decision node are easy to construct once a (diagnostic or therapeutic) plan is adopted.  The fact that no such a tree has been published by NIH or CDC or AMA or … means that they really don’t know what they are doing in fashioning Covid response policies – they have no agreed upon coherent approach.  (More evidence that science does no speak with a single voice.)  Such trees can be used by everyone, including people of modest intellect, to decide whether they need further medical attention or just continue self-observation and apply available at-home therapeutics.  They can also be versioned, and new versions can be published as newer/better data becomes available and/or process knowledge is updated.

[22dec21 update]  Here is a Covid decision tree designed by the school nurse at the Bear Creek School in the Seattle area.  People understand the utility of these decision aids, and are starting to generate them for their own organizations.  This one is for two categories – vaccinated and unvaccinated – of students.  H/T to our daughter who works at Bear Creek School for sending this down.  Now if we could only get the CDC or NIH off their collective butts and publish such a tool for the general population, it would sure turn a lot of heat into light.