“Inflation is always and everywhere a monetary phenomenon in the sense that it is and can be produced only by a more rapid increase in the quantity of money than in output.” Milton Friedman
George Rebane
“The time has come,” the Walrus said, “To talk of many things: Of shoes—and ships—and sealing-wax— Of cabbages—and kings— And why the sea is boiling hot— And what inflation brings.” (with apologies to Lewis Carroll) And more specifically we need to be forewarned that inflation is like “the fog, that comes on little cat feet”, and then surreptitiously consumes our plans for the future.
Most people know that the government, through our Federal Reserve, controls the “quantity of money” which pursues available goods and services in our economy. Fewer know that inflation is really an additional tax on your assets, which for their procurement you already have paid taxes on the inflated income. Inflation is then another tax, more insidious and mostly invisible that takes buying power out of our pockets and transfers it into the hands of government politicians and their bureaucrats. And it is they who get the benefits of ‘new money’, because those who get to spend it first, spend it with the value of the ‘old money’ before dilution sets in and the markets react. By the time you get it, prices have already reflected the additional dollars chasing the same goods and services.
The blame for the return of inflation is ours. It is we who voted in the conmen who promised us all kinds of goodies that would cost us nothing – it was always the other guy who would foot the bill. And we have kept doing it year after year.
The other tax that inflation brings is the usual tax that doesn’t even need to be raised, at least for a while until we’re convinced that our government needs to make even more “investments” in our behalf. The usual tax bill, not only goes up in nominal dollars, but also increases in the so-called ‘bracket creep’ which puts our inflated dollar amounts into the next higher rate categories.
In the final analysis, as we have said here for years, the dollar must be destroyed in order to satisfy all the obligations – now amounting to over $100T – that must be repaid in nominal dollar amounts. That means that the dollar’s buying power has to be reduced essentially to zero in order to legally satisfy and defraud our creditors, many of whom are actually ourselves. The ONLY thing that will save the dollar is an economy that grows at a rate which keeps the current debt levels at a low relative amount to our economy. Elsewhere in these pages I calculated this annual growth rate to be at least 5%, and that means at least 5% GDP growth year after year with no end in sight. No economy of our size has ever achieved such a steady state of high growth, and there’s no hope of our achieving it with socialists – who are rock apes when it comes to economics – in charge of our national weal.
In the meantime, and apropos the above, I’d like to leave readers with some means of penciling out their own estimates of how inflation will impact them. Let’s first do away with the commonly cited formula for calculating the actual buying power that appreciates with a portfolio’s annual nominal return of R% in an economy inflating at I%. That formula for inflation-adjusted return is usually given as RI = R – I, and it is wrong. The correct formula is RI = (R – I)/(1 + I), a significant correction when planning for retirement or future college expenses. The formula illustrates how inflation is an ‘invisible’ yet existential tax on assets. Note that the inflation-adjusted RI will be negative when I > R.
If we now include the impact of an overall tax rate of RT on our investment return R that is already impacted by inflation I, then the inflation/tax-adjusted return reduces to RIT = [R(1 – RT) – I]/(1 – I). At this point we can ask, what investment return must we obtain just to maintain the buying power of our original portfolio amount? This augmented return turns out to be R0 = I/(1 – RT) after we set RIT = 0.
A numerical example will serve to clarify these straightforward formulas which you can play with in a spreadsheet. Suppose you take as income your portfolio’s return of R = 10%, inflation comes in at I = 5%, and you pay an overall tax rate RT = 20%. Converting percents to decimals gives us the common but wrong inflation-adjusted return of RI = 0.10 – 0.05 = 0.05 = 5%. The above correct pre-tax formula yields RI = (0.10 – 0.05)/(1 + 0.05) = 0.0476 = 4.76%, almost a quarter percentage point lower.
And finally, when we include the impact of taxes, then adjusting for both inflation and taxes gives the actual appreciation as RIT = [0.10*(1 – 0.20) – 0.05]/(1 + 0.05) = 0.0286 = 2.86% – ouch! That is your portfolio’s actual increase in buying power when burdened by both inflation and taxes. To see how much return on our portfolio is required just to maintain its original buying power, we calculate R0 = 0.05/(1 – 0.20) = 0.0625 = 6.25%.
To appreciate how lucrative this double taxation is for our politicians and bureaucrats, consider that the effective tax rate RTE that you pay on the buying power of your return R is not the nominal RT with which you calculate your IRS tax bill. Instead RTE = (R – RIT)/R which with our example numbers calculates to RTE = (0.10 – 0.286)/0.10 = 0.714 = 71.4% – double ouch!! And this is the buying power that the government gets from the earnings on your investment, and/or from your annual wages for that matter.
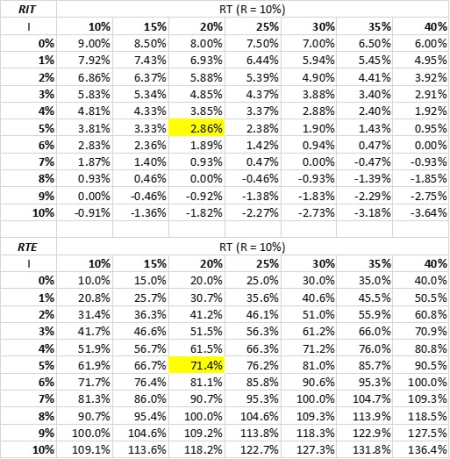
For a bigger picture of the lay of Total Tax Land, when we include explicit taxes on the resulting nominal income’s buying power reduced by inflation, the results are given in the tables below. The first calculates RIT, the percent change in the actual buying power from a return of R = 10% as a function of tax rate RT and inflation rate I. As an example, I’ve highlighted the 2.86% entry that remains from inflation I = 5% and RT = 20%. Note with what I and RT combinations your buying power is actually reduced.
The second table illustrates the behavior of RTE, the effective tax rate on the buying power of return R = 10% as the nominal tax rate RT and inflation I vary as shown. Again, I highlight RTE = 71.4% at I = 5% and RT = 20%. As the first spender of new money from the inflated money supply, RTE is the effective tax rate that the government extracts from the economy for its own spending programs. We again see that above certain values of inflation and nominal tax rates the government will actually diminish the buying power of your asset base as RTE rises above 100%.
You can use the above provided formulas to calculate RIT and RTE for other values of the rate of return R.
The derivation of the presented formulas is not rocket science, and should be accessible to anyone who remembers their middle school algebra classes. I will be glad to append the derivations as reader interest warrants. In any case, I hope that readers who made it to the end have had an eye-opening experience and found the material informative. (But there’s more. In a future post we’ll examine the impact of proposed taxes on assets and unrealized appreciation. Oi weh!)


Leave a comment