George Rebane

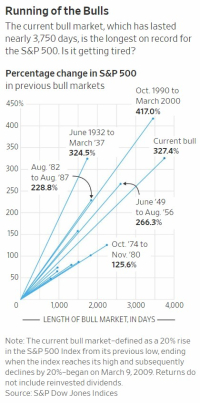We are now in the longest bull run in the history of America’s security markets. The nearby figure filched from the 15jun19 WSJ provides some perspective.

The question on everyone’s lips is when will this bull run end. As readers know, I’m a semi-retired successful entrepreneur and capitalist who has managed his own securities portfolio for decades, has recently focused on financial engineering, and still enjoys inventing and coming up with new squigglies in that field. One of my recent contributions has been the extension of Gott’s theory that probabilistically treats the future termination of minimally known processes. This extension was described here in – ‘…, and this too shall pass’ – on 10 November 2014.

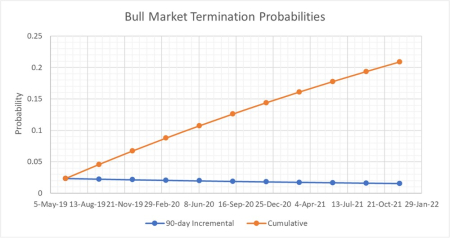
Well, it turns out that stock market bull runs are exactly the kinds of minimally known processes that succumb to the expanded R-G theory – all we reliably know about the bull market is its current age. So we can now ask more interesting questions such as, ‘What is the probability that the bull market will end in any future quarter (three-month period) starting now?’

The answer to that question is shown below for the next couple of years.  The blue dots/line indicate the diminishing probabilities that the bull will end in the quarter starting then, and the red dots/line indicate the growing probability that the bull will end sometime between now and the date shown.  (click on figure to enlarge)

Should there be more astute investors reading this, a natural extension of the above question is ‘How can we update such a probability when later we get some new information that bears on the markets?’ The good news is that this question can also be answered by using a form of the Bayes formula in which the then computed R-G probability serves as the ‘Bayesian prior’ from which to calculate the new (posterior) probability of the process about which we now know more than its age. The Bayes formula (described here) should be used thereafter as more pieces of relevant information are obtained. Fun stuff if you’re a bettin’ man (or woman).