George Rebane
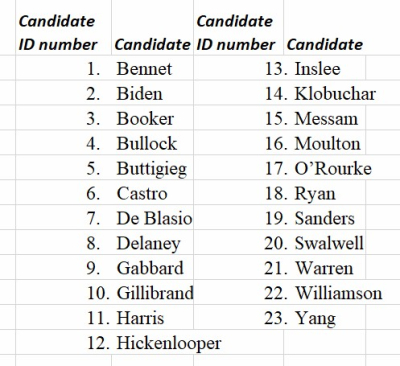
By last count there were 23 Democrat declared candidates running to become the next POTUS, with two more standing in the wings making up their minds. And here they are –
Now it doesn’t take rocket science to figure out that all but a handful will make it through the debates and primaries, and to the convention floor. One by one, most of them will start dropping out of the race for one reason or another. And it occurred to me that trying to noodle the order of such casualties over the coming months would be much like filling in the March Madness basketball championship playoff brackets. Only here it would be even simpler, and involve just making a list from the first to drop out all the way to the last one surviving as the 2020 Democrat candidate.
Any such list can be compared to the actual dropout sequence, but how do we compare two such lists to see which one was from the more astute (or lucky) prognosticator. In other words, how do you score various competing lists as to their accuracy? As a longtime game inventor, I love problems like this, and a solution didn’t take long to figure out. Start with sequentially numbering the candidates, say, in alphabetical order. A dropout list would then consist of the first 23 integers in some specific order.
Consider now that the Democratic National Convention is over, and we have at hand the actual dropout order of the candidates with the last one being their nominee for President. If we compare someone’s competing dropout list to the actual dropout order, then there would be differences in the actual vs predicted locations in the two lists. And the score of the predicted list should depend on how many and how large were the differences. A perfect score would be obtained by a list that perfectly matched the actual list, giving zeros for all the differences.
The maximum difference between a predicted and actual dropout location for a candidate would be the length of the list minus one – e.g. candidate X was predicted to be nominated, and instead turned out to be the first to drop out. Here such a difference for X would be 23 – 1 = 22. Now, say, candidate Y was predicted to be the ninth dropout, and, in fact was the fifteenth to leave the race, then that difference would be 15 – 9 = 6. And, of course, if candidate Z was predicted to drop out eighteenth and did indeed was the eighteenth dropout, then his difference would be 18 – 18 = 0. So, it is seen that such differences are actually penalties for wrong predictions.
The merit of each prediction then would be the complement of a candidate’s difference and its maximum possible value, here 22. The above candidates X, Y, Z would then contribute scores of 0, 16, and 22. As the campaign proceeds and candidates start dropping out, we can now always compute the percentage score for any given list of predictions – simply add the scores of the departed candidates, and divide by 22 times the number of the dear departed. This scoring process will allow the comparisons of competing lists as the campaign progresses right through the convention. A graph of such competing list might be interesting to track.
The competition could be made even more interesting if competing prognosticators were allowed to reorder the surviving candidates, say, at the end of 2019, and then again at the end of the last primary. Plots of such a competition could even engender interest enough to negotiate a side bet or two.
We’ll now number the 23 Democrat candidates in alphabetical order.
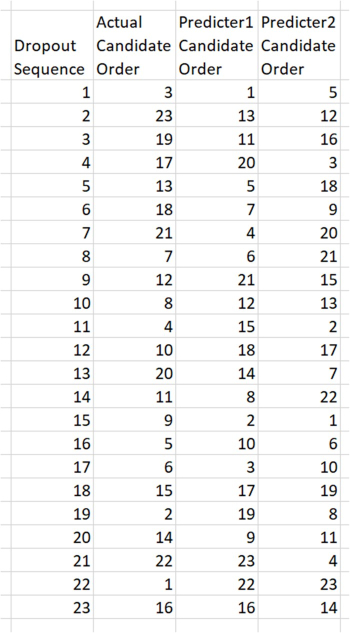
To illustrate the DropOut Derby competition, let’s assume that the actual order of dropouts is recorded sequentially as the weeks and months pass to Democrat convention and nomination. I wrote some code that allows us to simulate what such a competition of prognosticators would look like. The illustrated ‘actual’ and predicted sequence of candidate ID numbers were drawn at random to illustrate the format of the competition. Here is the results array showing also the predicted sequences by two competitors.
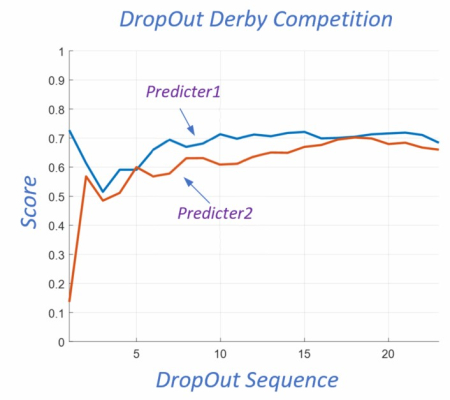
Given the ‘actual’ dropout sequence by candidate ID numbers, and the competitors’ prognosticated sequences, we then compute the scoring described above and show a plot of the scores over the entire 23 candidates as below (recall that the last ‘dropout’ is the Dems’ nominee). Of course, I would redraw and post the plot only as candidates dropped out, which would show the progress of the score lines progressing from left to right over the coming months.
So, I invite readers wishing to participate to post their sequence of the 23 candidate IDs in the comments, which I will then duly record, track, and report. Entries will be accepted until the first of the 23 drops out.
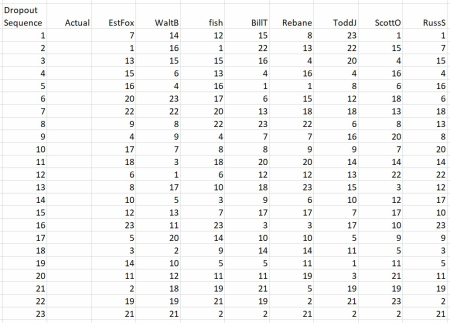
[6jun19 update] The entries to date are shown below.



Leave a comment