George Rebane

OK boys and girls, time to take a break from our usual work of solving the world’s socio-political problems.  Today we’re going to look at a new and, hopefully, better method for scoping your rifle.  I am a lifelong shooter and also a military and NRA trained range safety officer (RSO).  As a longtime member of our local Sportsmen shooting club (rifle, pistol, trap, archery), I do my required club work hours serving several times a year as the rifle/pistol RSO on Sunday afternoons when the club opens its outdoor range to the public.

You shooters can imagine the stories I have stored up over the years helping (the mostly inexperienced) shooters and keeping them from accidentally killing someone.  Well, one of the tasks I’m frequently asked to help with is scoping the rifle of a guest or member who is not quite clear on the concept.  To scope a rifle means to align the scope with the rifle’s barrel so that a shotgroup’s centroid is close to the center of the bullseye at a given range (say, 100 yds) when shot with the scope’s crosshairs, or point of aim (POA), centered on the bullseye.

The scope itself is attached to the rifle via a carefully positioned mount screwed firmly to the top of the rifle’s receiver (action), preferably by an experienced gunsmith.  Then the scope itself is attached to the mount and positioned in azimuth and elevation so that its crosshairs are approximately centered on the target when the target is approximately centered ‘within’ the bore of the rifle.  This is achieved by strapping the rifle to a shooting sled and taking out its bolt so that you can look through the bore at the target.  The sled is adjusted to align the rifle’s bore.  Then the scope’s A(zimuth) and E(levation) knobs are turned so as to put the crosshairs on the target.  (Aligning the bore of semi-automatic rifles is a bit trickier and can be achieved with various fiber optic gadgets and mirrors, or just looking over and to the side of the barrel to visually align the bore.  Such an alignment is best done at a shorter range, say, 25 yards.  You can declare victory at this stage when you fire a scoped round at 25 yards, and it hits the paper somewhere on the target, preferably near the center.  Now fasten the scope’s mounting screws, and you’re ready for the real work of putting lead on target.  Again, you can have all this preliminary work done by a trusted gunsmith, and immediately proceed to the next phase.

Before we talk about procedure (or the scoping algo, if you wish), the shooter needs to know a bit about the built-in random stuff that is involved in getting a group of rounds (shotgroup) into the bullseye.  The random things exhibit themselves as a scatter of shots or points of impact (POIs) when you hold everything constant at the shooting table.  First and foremost is the size of the shotgroup (usually at 100 yards) claimed/advertised by the rifle’s manufacturer.  This is the smallest shotgroup possible with the rifle and specified ammunition when you pour the rifle into a huge cement block and fire your shotgroup.  They don’t actually encase the rifle in cement, but you get the idea.  Your results will vary, but use their numbers.

From here on I will be using numbers from my Remington Model 700 30-6, scoped with a Nikon ProStaff 6732 4-12X40 Mil-Dot.  This is about as run-of-mill American large game rig as you can buy; nothing too fancy, yet demonstrably reliable over the years.  The only thing that the average hunter doesn’t usually buy is a scope with a Mil-Dot reticle in which the dot spacing on the crosshairs is in mils.  (As ex-military, and a trained cannon cocker, how would I look if I got a scope with the standard ‘minute of angle’ (MOA) reticle for civilians who haven’t clue about how to use the WoRm formula?)  No matter, Mil-Dot and MOA scopes work equally well for what we’re about to do.  Just to make sure, recall that there are 360×60 = 21,600 minutes of angle in a full circle.  And there are 2π = 6.283 radians = 6,283 milliradians in a full circle – remember, radians are the natural measure of angle, degrees are an arbitrary measure that divides the circle into 360 equal parts.  And each degree is further divided into an arbitrary 60 number of minutes of angle, each of which in turn is again divided into an arbitrary 60 number of seconds of angle.  (Actually, these divisions are not all that arbitrary once you define a nautical mile as subtending one minute of angle from the earth’s center on a great circle route.)  Long ago the military decided to divide the circle into 6,400 parts called mils.  They figured correctly that 6400 mils is close enough to 6283 milliradians for government work like killing people and navigating.  Besides 6400 is easy to remember and divides by two a whole bunch of times into nice even numbers (for the tech nerds 1 mil = 0.982 milliradians).  Using the WoRm formula allows you to quickly compute range to an object of known size, or the object’s size if you know its range.  (more here)

Almost all rifles like mine are advertised to have a shotgroup spread (or radial sigma) of around 0.25 inches at 100 yards (which will be our range to target from here on out).  For the calculations to follow, I have taken the shooter’s contribution to the POI’s random scatter as contributing another 0.50 inch sigma.  When you ‘add’ these together and compute the resulting ‘circular error probable’, you get CEP = 0.658 inch radius.  This number is important, because that is the best that you can do with your rig and your shooting ability.  Specifically, a CEP circle around the bullseye is one into which 50% of the fired rounds will impact.  Your objective here is to scope your rifle with the minimum number of rounds so that the centroid of your last shotgroup falls reliably into the CEP centered on the bullseye.

[Skip this part included for techies.  If we examine the POI distributions in the A and E directions, they invariable turn out to be bell curves (gaussian pdfs).  However, the shotgroup’s distribution of POI radial distances from the centroid turns out to be described by the Rayleigh distribution familiar to physicists and other squiggly pushers.  This is an asymmetrical distribution for positive numbers that has one hump and trails off to zero as the distance increases – look it up (here).  The math required to translate bell curve sigmas, actually variances, into its Rayleigh variance and then into the CEP radius gets a bit complex, but nothing you can’t do in a spreadsheet.  The above noted sigmas and the CEP radius result from such Rayleigh distributed shotgroups.]

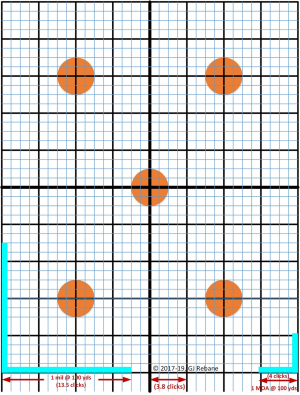
Now, with these preliminaries out of the way, we can start the scoping procedure.  Place your target at 100 yards, and set up your rifle in the sled so that it’s easy to put your crosshairs or ‘point of aim’ (POA) anywhere on a letter size (8.5×11) target sheet.  It is best if the target is made specifically for scoping a rifle.  Since I haven’t been able to find the exact design that I consider to be most helpful in this task, I designed one myself which is shown below, and the PDF of which you can  Download Target_1inGridannotated . Just be sure when you make copies, that the one inch squares remain one inch squares.

The target has five one-inch diameter bullseyes and is laid out on a quadrille field of one-inch squares.  On the lower corners I have placed bars that subtend 1 mil in A and E (lower left), and 1 MOA (lower right).  Most scopes can be adjusted in ¼ MOA increments or clicks on the scope’s A and E knobs, so it takes 4 clicks to move the POA one MOA in either direction.  (It takes 13.5 clicks to move the POA one mil.  Of course, the scope cannot be moved a fraction of a click, so you must always decide and note whether your adjustment was ‘over’ or ‘under’ when going through the scoping procedure.)  I have made my own target frame out of PVC pipes so that it holds a two pieces of cardboard, each of which can fit four of the targets shown above.  When doing such precision shooting – actually any target shooting – always have another copy of the target on the shooting bench by your elbow, and note the most recent POIs on it.  With the quadrille field that is an easy task, and it lets you do your noodling for computing centroids and adjusting the scope in a more stable and calm environment than continually having to peer through the spotting scope or your rifle scope.  And when you’re finished, you have a permanent record of how the whole rig performed as you brought it on target.

The standard procedure for scoping is to ‘chase the centroid’ of your shotgroup with the cross hairs.  In this scheme your POA is always the bullseye, but your POIs form a, say, triangle that is usually off in some direction from the bullseye.  That means that you fire a group, usually three rounds, and then adjust your scope in A and E to move the crosshairs from the bullseye to the centroid.  The next group is fired again with crosshairs on the bullseye, and the scope is again adjusted to the centroid of the new shotgroup.  This process is repeated and results in the reduction of the centroid-bullseye distance until the shooter decides that his centroid is close enough to the center of the bullseye.  Here I recommend using the size of the orange bullseyes as being close enough to a typical rifle/scope’s CEP.  When you put the centroid into the orange, you can declare total victory, reset the A and E knob scales to zero on your scope, pack up and go home.

Computing the centroid.  You can, of course, eyeball it.  But since you’re using my nifty target, you can just pick off the coordinates of the POIs by arbitrarily making one nearby intersection of the heavy lines into the coordinate origin (i.e. 0,0) and noting down the relative x-coordinates and the y-coordinates of the POIs in that coordinate system.  Sum the x-coordinates and divide by the number in your shotgroup, here three.  Do the same for the y-coordinates, and then mark the centroid on your bench target – see how easy that is to have one target for all these calcs right by your elbow.

With your centroid marked, you can just read off the x and y distances from your POA bullseye and translate those inches into A and E clicks.  Remember, you are chasing the centroid out from the bullseye.  So if your centroid was 3 inches to the right of the bullseye center, and 2.5 inches above the bullseye, then with 4 clicks/inch you’d dial in 12 A-clicks to the right, and 10 E-clicks up.  When your centroid calculates into the orange, you’re done.  However, most shooters will want to fire a confirmation shotgroup, if for nothing else than just to feel good about their work.   Here you might run into a bit of consternation if your confirmation centroid falls outside the orange bullseye.  What to do?  Should you again reach for the A and E knobs?  No, don’t do it because what you witnessed was the luck of a random draw from the Rayleigh distribution.  Leave it as is, and fire another shotgroup if it’ll make you feel better.  That centroid should be back in the bullseye.  But there’s a better strategy here that will almost guarantee that once you’re in the CEP, you’ll not drift out of it on you next shotgroup.  I’ll describe that directly.

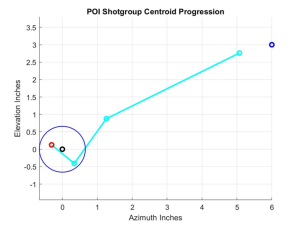
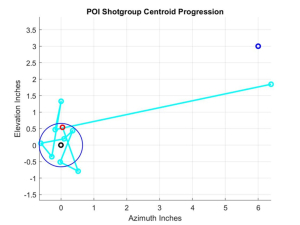
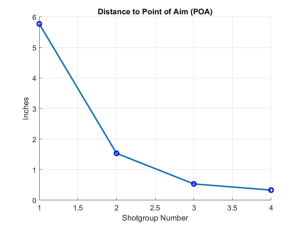Just a word of background in the development of this new and improved method to quickly get into the CEP with the minimum number of rounds expended.  I asked myself if there were a better way than chasing the centroid with 3-round shotgroups.  To answer that, I wrote a simulation program (natch!) that did the proper sampling of the probability distributions and actually computed the centroids of N-round shotgroups repeated M times to see how the distance to bullseye behaved starting from arbitrary distances from the bullseye.  I programmed the graphics to illustrate a number of the outputs, two of which I illustrate here below.  The first is a plot of an actual (‘Monte Carlo’) trial of the centroid to POA (bullseye) distance for each succeeding shotgroup.  The second is the actual location of the centroids as they approach the bullseye located at (0,0) as indicated by the little black circle and surrounded by the blue CEP circle described above.  The little blue circle at (6,3) inches was the arbitrary starting point, before adjustments, marking the centroid of POIs if we fired a bunch of rounds with the POA being the bullseye – i.e. the little blue circle marks the starting off-distance between the rifle’s bore and scope’s crosshairs.

The cyan colored line with its little circles marks the progression of the shotgroup centroids.  The figure shows the results of a trial with three shotgroups.  And now for the punch line.  It turns out that the better strategy is not to chase the centroid with multi-round shot groups, but instead to first fire one round, and then make the big correction by initially measuring the coordinates (here 5.1,2.75) of that round and correcting fully for to put the next centroid in the bullseye.  With this adjustment, we subsequently fire a 3-round shotgroup, and plot its centroid as shown (here 1.3,0.9).  However, this next shotgroup is not corrected fully to the bullseye, but corrected only to about 0.7 of the distance to the bullseye.  In a practical sense you can use 0.75 or ¾ of the distance to the bullseye.  That means you calculate the usual number of A and E clicks required to get to the bullseye, and then multiply each click count by 0.75 or ¾.  It turns out this prevents overshoots but still allows you to approach the bullseye very rapidly.  In this case it only takes 13 rounds and three A/E adjustments, and you’re done.

So the recommended policy to quickly reduce the centroid-to-bullseye distance to less than the CEP radius, you apply the following algorithm.

1. Fire one round at the bullseye and note its POI.
2. Compute and apply the A and E clicks required to put the next POI in the bullseye.
3. Fire a three-round shotgroup.
4. Compute its centroid and apply ¾ of the A and E clicks required to put the next POI in the bullseye.
5. Repeat steps 3 and 4.
6. Repeat steps 3 and 4 if the new centroid is not within CEP, else stop.

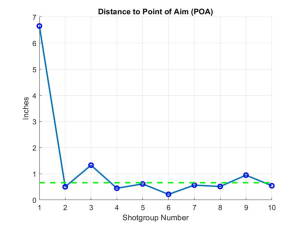
Some still argue that the more shotgroups you shoot, the better will be you scope adjustment.  That is not true for the simple reason that once you get within the dispersion error boundary of your rig plus aiming skill, you’ll just randomly dither around the bullseye (as shown below) without making any statistically significant progress – in short, you’ll just be wasting rounds until you serendipitously get a centroid on or near the dead center, and then think you’ve put one over on the great god Ran-Dom.  Here’s what such a policy typically looks like with a ten shotgroup effort.  (The dotted green line in the figure below is the CEP radius.)

[This post may be downloaded as a PDF document –  Download Scoping Your RifleA.]