George Rebane
[This little interlude will most likely interest very few RR readers, but it has provided me a respite from the political struggles through my continuing love-affair with pushing squigglies. Truth be told, I do this kind of stuff quite often, and who knows, there’s always the off-chance that some reader may show interest.]
As we sat last Saturday morning waiting for the history making Senate confirmation vote on Judge Kavanaugh, I meandered across yet another article on the supervolcano that rumbles under Yellowstone National Park. Geologists tell us that the volcano has erupted every 600K – 800K years or so with a devastating effect that we in recent decades have come to call a ‘nuclear winter’. The last one occurred about 640K years ago. When that magma dome blows again it will put so much dust, dirt, and ash into the earth’s atmosphere as to change the earth’s climate for several years starting with a two- or three-year winter that will kill much of the planet’s vegetation and critters, make agriculture near impossible, and therefore cause the wholesale death of most of us who live here – at least that’s what NASA and a covey of paleo-geologists tell us.
It turns out that modern technology today can provide a very beneficial prophylactic to prevent such an event, and in the process generate a considerable amount of clean geothermal electricity. Scientists at NASA tell us that it would be possible to cool the molten magma bubble by drilling laterally into its sides, pumping down cold water, and harvesting super-heated steam for electricity generating powerplants on the surface.
The cost of drilling such 10km deep holes comes to almost $3.5B, add another few billion dollars to the budget to put up a powerplant or two, and you could see doing the whole thing for about $10B while lowering or completely eliminating the risk of a big blow-up. The cost of the electricity generated in this manner comes to about $0.10/kWh – cheap at twice the price. So why aren’t utilities rushing in there to do just that? (more here and here)
Well, the best anyone can tell is the high business risk of such an undertaking in a national park that is surrounded by high walls of environmental regulations manned by legions of super-zealous, lawyer-ladened, eco-nazis with a paucity of critical thinking skills. Now this is where government should step in and play the crucial role of paving the way to implement such a humanity-saving insurance policy with a clean energy solution to boot. But so far no one on either end of Pennsylvania Avenue has made a peep about this. It can’t be the cost, because the feds lose more than $10B a day with what they drop off their loading docks. So, for an answer, let’s look at the risk side of this potential earth-shaking catastrophe.
To quantify the downside risk we techies first appeal to what is called probability rate theory that is a well-known tool in areas like search and detection using radars and sonars. The best estimate of Yellowstone’s catastrophe rate is once every 700K years. That’s about the average frequency at which the big magma bubble gets close enough to the surface for its outward pressure to blow its top.
The real question we have to answer today is something like ‘what is the probability that Yellowstone blows again in the next 100 years?’ Clearly, if that probability, let’s label it P100, is sufficiently high, we should get busy tout de suite on the drilling and powerplant project described by NASA. I have no idea what is ‘sufficiently high’ for the congress critters to get something going. Most certainly if P100 = 0.5, then things in Washington would start happening. But if P100 = 0.01, then I think we would continue to sleep on it a bit more. So what is the real value of P100?
Lucky for you dear reader, mom sent me to school to learn how to answer such questions. So I’ll save you the trouble of reading my brilliant analysis before calculating the answer, and give it to you right off the bat – P100 = 0.000246. That’s a pretty low number for the next supervolcano eruption to take place sometime in the coming 100 years, and it pretty much explains why people aren’t getting too excited about it in the government or in the energy industry.
Now that doesn’t mean we won’t have one of those smaller eruptions that occur every few 10K years, these will not be civilization enders, but they might screw up our agriculture on the Great Plains for a few years. Maybe later, if there’s available data, I’ll do some noodling on the chance that a ‘minor’ eruption will happen in the next century. So the question remains, why are the NASA people getting excited about Yellowstone’s civilization ending volcano?
%%%%%
OK, now for the brilliant analysis that produced the answer (full disclosure – actually any techie with the basics in estimation theory under his belt could do this). First, we must characterize the Yellowstone supervolcano ‘process’. Its big eruptions started around 2.5M years ago and have occurred every 600K to 800K years since then. We assume along with NASA that this top-blowing process is still both ongoing and stable. If the intervals could not be so bracketed from geological data, then the eruptions could have occurred at any time with, say, a mean interval of 700Ky. This would have meant that it behaved like a ‘memory-less’ process with an appropriate exponential probability density function (pdf) describing the eruption intervals.
Here our mean arrival frequency is lam = 1/700Ky, a pretty small number (the appropriate exponential pdf is then f(T) = lam*exp(-lam*T). The probability of n eruptions in a period of T years is then given by the so-called Poisson arrivals formula, P(n) = (exp(-lam*T)*(lam*T)^n)/n! for n = 0,1,2,… . Here we want to find out what is the probability of at least one super eruption in the next century, i.e. T = 100y. A little thought reveals that the required P(n>0) = 1 – P(0), meaning it’s the complement probability of no eruption in the next 100 years. Putting the formula in a spreadsheet gives us P(n>0) = 0.000143 or a bit more than one chance out of ten thousand that Yellowstone will blow in the next hundred years. Now no one is going to get excited about some chance that’s between slim and none.
But the Yellowstone supervolcano eruption process is not memory-less; in fact it has a very definite memory of when the last time pressure build-up was relieved from the top of the magma bubble as witnessed by the relatively tight 200Ky time brackets in which such eruptions have occurred. So we can’t use the above result.
Before developing the correct answer, I want to point out another way we could have computed P100 if all we know about a process is how long ago it started, and nothing else. Such a process in this case would be one that started 640Ky ago (at the time of the last eruption) and is characterized by an ongoing and unknown mechanism that has produced no super eruption. The question for such minimally known processes can be formulated as ‘what is the probability that an X-(time unit) old process will stop in the next Y (time units)?’ The answer is given by the straightforward Gott-Rebane formula (more here) P(Y) = Y/(X+Y). In our case P(100) = 100/(640K+100) = 0.000156, an answer not too different from the memory-less answer above. But again, it’s an answer we cannot use because we do know much more about the process than that to which the application of Gott-Rebane requires. So now we head for the final roundup.
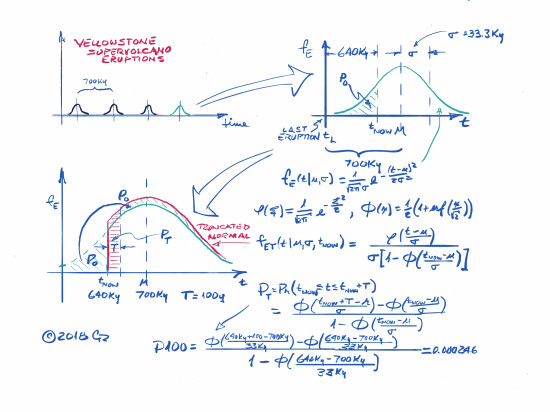
In our universe, the combination and confounding of almost all random processes wind up with a pdf that looks a lot like the Gaussian bell curve, and it can be shown mathematically that combining a bunch of pdfs of different shapes actually does result in a Gaussian, normal, or bell curve pdf. To cut to the chase, our eruption intervals look very much like they are drawn from a pdf with a mean of 700Ky and a 200Ky six-sigma bracket that defines its standard deviation to be sig = 200Ky/6 = 33Ky. These periodic eruption bell curves are shown in the upper-left of the figure below (forgive my scribbles).
Today we are well into the Gaussian or normal probability density function (pdf) that is the last and green bell curve in the series. It is labeled fE and expanded in the upper-right of the figure that shows the shaded probability mass P0 of this bell curve that is already behind us. What then remains is an updated pdf that is a truncated version (shown in red) of the fully formed (green) bell curve in the lower-left part of the figure. The area under the truncated red one must also equal unity or certainty that it still describes when Yellowstone will blow. That requires us to take the ‘passed’ probability P0 and spread it proportionately over the top of the truncated pdf now labeled fET. For the mathematically versed, these pdfs are shown in the lower-right of the figure along with the skeleton development of the equations required to answer our question – i.e. to compute the value of P100 which is the probability that Yellowstone will have a super eruption some time during the next century.


Leave a comment